 Gesamtliste der
Modelle Gesamtliste der
Modelle
|
|
Das
Runge-Kutta Verfahren
|
|
|
|
| Die
Aufgabe:
Numerische Lösung
einer Differentialgleichung
(eines Anfangswertproblems) |
|
Von einer Zustandsgröße Z
seien bekannt:
-
der aktuelle Wert Z(to) zum Zeitpunkt
to, d.h. anschaulich: ein Punkt
A(to;Z(to)).
-
eine Differentialgleichung
Z'(t) = f ( t ; Z(t) )
für die momentane Änderungsrate Z'(t)
bzw. - anschaulich gesprochen - für die
Steigung m=m(t)=Z'(t) zu einem beliebigen Zeitpunkt t
.
|
Das Ziel:
Verbesserung des Euler-Cauchy-Verfahrens zur Bestimmung von
Prognosewerten |
|
Aus den obigen Angaben ( Punkt A und Steigung
m=m(to) im Punkt A ) lässt sich mit Hilfe des
Steigungsdreiecks eine lineare Funktion P (Tangente im Punkt A) ermitteln,
deren Wert P(to+dt) nach dem
Euler-Cauchy-Verfahren als Prognosewert
für Z(to+dt) dient.
Im allgemeinen wird jedoch der Graph von Z im betrachteten Zeitintervall
dt mehr oder weniger beträchtlich von seiner Tangente abweichen,
so dass der Wert P(to+dt) nur einen recht ungenauen Prognosewert
für den vorherzusagenden Wert Z(to+dt) darstellt.
Insbesondere bei langen Prognosezeiträumen (vielen Prognoseschritten)
wird sich der Verfahrensfehler schnell vergrößern. |
|
| Der Ansatz
des Runge-Kutta-Verfahrens |
|
Aufbauend auf dem Euler-Cauchy-Verfahren kann man
- so Runge-Kutta - den gesuchten Prognosewert nur dadurch
grundsätzlich verbessern, dass man den für die lineare Fortschreibung
Z(to+dt) = Z(to) + m(to)*dt
benutzten Steigungswert m nicht nur aus der anfänglichen
Steigung Z'(to) bestimmt, sondern von dem (mittels der gegebenen
Differentialgleichung bekannten) weiteren Steigungsverhalten der Funktion Z
abhängig macht, indem man zunächst mit einer gewissen Teil-Schrittweite
"Hilfsprognosen" erstellt und schließlich die dabei gewonnenen
"Hilfssteigungen" passend mittelt. |
| Runge-Kutta-Verfahren
4.Ordnung |
|
Das hier dargestellte Runge-Kutta-Verfahren 4.Ordnung
verwendet dabei "Halbschritte" im Zeitintervall dt und gewinnt dadurch
4 "Hilfssteigungen" m1, m2, m3,
m4, deren gewichtetes arithmetisches Mittel
m =
1/6*(m1+2m2+2m3+m4)
dann die zur linearen Fortsetzung der Funktion Z benutzte Steigung
darstellt. Durch die doppelte Gewichtung der beiden "mittleren
Hilfssteigungen" m2 und m3 wird
dabei i.a. ein durchaus spürbarer zusätzlicher Genauigkeitsgewinn
erzielt. |
| Das Verfahren
im einzelnen |
|
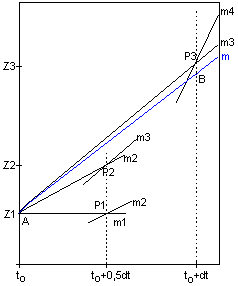
Zur Illustration des Verfahrens dient als Beispiel
die Differentialgleichung
Z'(t) = Z(t) + t -1
mit dem Anfangswert Z(0) = 1
und der (untypisch großen!) Schrittweite dt=1.
Die eingezeichneten Geraden sind dabei jeweils mit ihrer
Steigung m bezeichnet.
Dieses Beispiel wird unten auch rechnerisch behandelt. |
 |
|
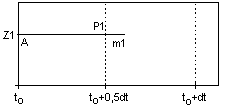
Mit der anfänglichen Steigung
m1=Z'(to) als
1. Hilfssteigung wird - ausgehend vom gegebenen Startpunkt
A - zunächst ein "Euler- Halbschritt" gemacht. Dadurch erhält
man einen
1. Prognosehilfswert Z1 = Z(to) +
m1*0,5dt. |
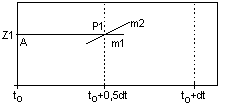 |
|
Man unterstellt nun, der zugehörige
Punkt P1(to+0,5dt;Z1) sei ein Punkt
des Graphen der gesuchten Funktion Z, und errechnet durch Einsetzen dieses
Punktes P1 in die gegebene Differentialgleichung die zugehörige
Steigung als
2. Hilfssteigung m2 = f ( to + 0,5dt ;
Z1 ). |
 |
|
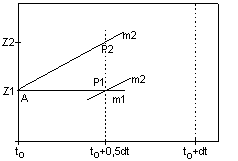
Mit dieser Hilfssteigung m2
führt man nun den ersten "Euler-Halbschritt" erneut durch und
erhält daraus einen
2. Prognosehilfswert Z2 = Z(to) +
m2*0,5dt.
Wieder unterstellt man, der Punkt
P2(to+0,5dt;Z2) sei ein Punkt des
Graphen der gesuchten Funktion Z, |
 |
|
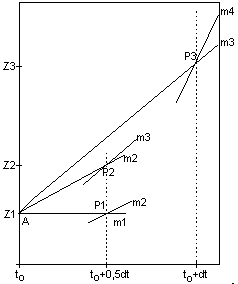
und errechnet durch Einsetzen des Punktes
P2 in die gegebene Differentialgleichung die zugehörige Steigung
als
3. Hilfssteigung m3 = f ( to + 0,5dt ;
Z2 ).
Mit dieser Hilfssteigung m3 führt man nun einen
ganzen "Euler-Schritt" durch und erhält einen
3. Prognosehilfswert Z3 = Z(to) +
m3*dt
sowie - wieder durch Einsetzen des als Kurvenpunkt interpretierten
Punktes P3(to+dt;Z3) in die gegebene
Differentialgleichung - die zugehörige Steigung als
4. Hilfssteigung m4 = f ( to + dt ;
Z3 ). |
 |
|
Aus den so berechneten 4 Hilfssteigungen
m1,m2,m3,m4 wird
nun das gewichtete arithmetische Mittel
m = 1/6*(
m1+2m2+2m3+m4 )
berechnet, das dann als Prognosesteigung bei der linearen Fortsetzung
der Funktion Z benutzt wird. Man erhält so beim
Runge-Kutta-Verfahren 4.Ordnung den
Prognosewert Z(to+dt) = Z(to) + m * dt
.
Der zugehörige Punkt B( to+dt ; Z(to+dt
) wird als der gesuchte "nächste" Kurvenpunkt prognostiziert
und dient als Startpunkt für den nächsten
Runge-Kutta-Iterationsschritt.
Wie sich die Funktion Z bzw. ihr Graph allerdings zwischen den Punkten A
und B genau verhält, bleibt unbekannt und könnte nur durch eine
Verfeinerung der Schrittweite näherungsweise ermittelt werden; dadurch
würde sich jedoch auch der Prognosepunkt B ändern. |
|
|
|
Und nun
die Rechnung ...
... für einen Prognose-Schritt
mit der Schrittweite dt=1 |
|
Gegeben sei - wie oben - die Differentialgleichung
Z'(t) = Z(t) + t - 1 mit Anfangswert Z(0) = 1.
Die Schrittweite dt=1 ist sicher untypisch groß gewählt - üblich
wäre etwa dt=0,1 mit erheblichem Genauigkeitsgewinn.
Sie ist aber gut geeignet, um anhand eines Vergleiches mit dem
exakten Wert und dem Prognosewert nach "Euler-Cauchy" die "Genauigkeit"
des Runge-Kutta-Verfahrens zu demonstrieren. |
| Exakte (analytische) Berechnung |
Das gegebene Anfangswertproblem
hat die Lösungsfunktion Z(t) = et - t , also ist der
exakte Funktionswert
Z(1) = e - 1 = 1,71828... |
| Prognose nach Euler-Cauchy |
m = Z'(0) = Z(0)+0-1 = 1-1 = 0 ,
also ist der "Euler-Cauchy-Prognosewert"
Z(1) = Z(0) + m*dt = 1 |
|
|
| Prognose nach Runge-Kutta |
m1 = Z'(0) = Z(0)+0-1 = 0
Z1 = Z(0)+m1*0,5dt = 1+0*0,5 = 1
m2 = Z'(0+0,5dt) = Z1+(0+0,5dt)-1 =
0,5
Z2 = Z(0)+m2*0,5dt = 1+0,5*0,5 =
1,25
m3 = Z'(0+0,5dt)=Z2+(0+0,5dt)-1 =
0,75
Z3 = Z(0)+m3*dt = 1+0,75*1 = 1,75
m4 = Z'(0+dt) = Z3+(0+dt)-1 =
1,75
m =
1/6*(m1+2m2+2m3+m4)
= 0,70833...
also ist der "Runge-Kutta-Prognosewert"
Z(1) = Z(0+dt)=Z(0)+m*dt=1+m= 1,70833... |
|
Ergebnisvergleich
bzgl. des Verfahrensfehlers
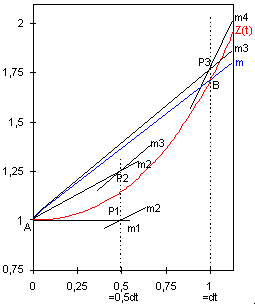
Trotz der großen Schrittweite ist die Prognose nach Runge-Kutta
bei diesem (allerdings "gutmütigen")
Beispiel sehr gut.
Der verfahrensbedingte Fehler gegenüber der exakten Lösung
beträgt hier nur ca. 0,01 , während er beim Euler-Cauchy-Verfahren
mit ca. 0,72 doch noch sehr groß ist.
Entsprechende, jedoch weit weniger krasse Befunde ergeben sich,
wie weitere (eigene) Rechenbeispiele zeigen können, auch dann, wenn
beim Euler-Cauchy-Verfahren die Schrittweite
deutlich verringert wird. |
|
Graphische Darstellung des Runge-Kutta-Verfahrens
4.Ordnung
mit eingetragener Lösungsfunktion
 |
|
|
|
| Grundsätzliches
zum Verfahrensfehler |
|
Typisch bei der Anwendung numerischer Verfahren
zur Lösung von Differentialgleichungen ist der sogenannte
Verfahrensfehler, der natürlich umso größer ist, je
größer die Schrittweite dt gewählt wird.
Die Theorie lehrt, dass ( für dt < 1 ) dieser
Verfahrensfehler bei Verwendung des Euler-Cauchy-Verfahrens von der
Größenordnung (dt)2, beim Runge-Kutta-Verfahren dagegen
lediglich von der Größenordnung (dt)5 ist.
(vgl. die einschlägige Fachliteratur; einen ersten Einblick geben z.B.
bereits "Lexika" wie:
Reinhardt,F.;Soeder,H.: dtv-Atlas zur Mathematik, Bd.2, München 1977,
S.390ff.
oder auch
Netz, H. (Hrsg): Formeln der Mathematik, Westermann, Braunschweig 1965,
S.546 ff). |
|
|
|
| Wer's genauer
wissen will ... |
|
Genauere Untersuchungen hinsichtlich der Auswirkungen
unterschiedlicher dt-Wahlen beim Runge-Kutta-Verfahren 4. Ordnung sind am
Beispiel des exponentiellen Wachstums zusammengestellt auf der Seite
Diskretisierung eines kontinuierlichen Systems
und numerische Lösung ... |
|
|
|
|
|
Der vergleichsweise große Verfahrensfehler des Euler-Cauchy-Verfahrens
nimmt i.a. mit wachsender Iterationszahl sehr stark zu, während
er beim (allerdings für diskrete Systeme im Grunde ungeeigneten)
Runge-Kutta-Verfahren meist auch über längere Zeiträume in
erträglichen Grenzen bleibt.
Jedenfalls leuchtet ein, dass aufgrund des deutlich größeren
Verfahrensfehlers das Euler-Cauchy-Verfahren allenfalls bei diskreten Systemen
(aufgrund der vorgegebenen Schrittweite) und/oder bei sehr kurzen
Prognosezeiträumen einigermaßen erfolgreich angewandt werden kann. |
| Gefahr von
Rundungsfehlern |
|
Andererseits steigt durch den deutlich erhöhten
Rechenaufwand sowohl bei Verwendung des Runge-Kutta-Verfahrens als auch beim
Euler-Cauchy-Verfahren mit verringerter Schrittweite die Wahrscheinlichkeit
von Rundungsfehlern spürbar an. |
| Fehlerüberlagerung
Wie man sich auch dreht und wendet, der .... bleibt
hinten! (Volksweisheit) |
|
Man kann also Fehler prinzipiell nicht vermeiden,
und es bleibt obendrein unklar, in welcher Weise Verfahrens- und Rechen-
bzw. Rundungsfehler den Gesamtfehler vergrößernd oder verkleinernd
beeinflussen. Es ist vielmehr durchaus möglich, dass sich die Fehler
bis zu ersichtlich unsinnigen Rechenergebnissen verstärken. Dies gilt
in besonderem Maße für periodische Abläufe, so dass hier leicht der Eindruck eines chaotischen Verhaltens entstehen kann, obwohl
dieses in der Realität gar nicht vorliegt. |
Vorsicht
!
Hier müssen Sie selber nachdenken! |
|
Auswahlprobleme mit
den Rechenverfahren
Unterrichtsprobleme mit den
Rechenverfahren
|